研究背景介绍
今天为大家介绍一篇基于多对比度核磁共振影像的无监督配准工作,这篇工作发表在2021年的IEEE TMI上。在本文中,作者设计了一种由仿射和可变形变换组成的端到端从粗到精的网络架构,还开发了双重一致性约束和基于先验知识的损失函数以提高配准性能。所提出的方法已在包含555个病例的临床数据集上进行了评估。与常用的配准方法(包括 VoxelMorph、SyN 和 LT-Net)相比,该方法在识别中风病变方面取得了更好的配准性能。此外,本文方法在相同的CPU上进行测试时,比最具竞争力的方法(SyN)快10倍左右。
文章信息
Weijian Huang, Hao Yang, Xinfeng Liu, Cheng Li, Ian Zhang, Rongpin Wang, Hairong Zheng, Shanshan Wang*, A coarse-to-fine framework for unsupervised multi-contrast MR image deformable registration with dual consistency constraint. IEEE Transactions on Medical Imaging, doi: 10.1109/TMI.2021.3059282.
发表链接:
https://ieeexplore.ieee.org/document/9354195
开源代码:
https://github.com/SZUHvern/TMI_multi-contrast-registration.
1. 简介
核磁共振成像(Magnetic Resonance Imaging,MRI)因为其极佳的软组织对比度以及多个成像序列提供互补信息,是活体大脑病理分析最常用的方式,常用于诊断和手术方案制定。具体而言对同一个患者进行不同序列的扫描,如T1,T2, DWI等,相对于单对比度可以更全面地评估一个人的生理结构以及功能特征。但因为病人在扫描过程中有可能运动,再加上扫描成像等系统问题(如扫描序列参数不规范、涡流导致的DWI图像变形等),扫描出的多对比度图像可能出现错位现象,从而对后续疾病的精准诊断与量化分析产生不利影响,因此,需要开发MR多对比度图像精准配准方法。
1.1 传统的图像配准方法
传统的图像配准算法,通常基于优化问题的迭代数值解。其中,SyN[1]是医学图像配准中应用最广泛的算法。它描述了一种基于欧拉-拉格朗日优化的对称图像归一化方法,用于最大化互相关。这些方法尽管获得了可观的配准结果,它们的效率仍然可以提高,因为它们通常都是基于每次迭代优化的[2]。
1.2 基于深度学习的单模态图像配准
随着深度学习领域的快速发展,一些基于深度学习的图像配准模型被提出。最开始是采用深度学习来增强迭代方法的配准性能。然后,引入深度强化学习来预测配准区域。近几年一项代表性工作是STN(空间变换网络),它生成密集的可变形变换来配准图像,并在仿射变换等方法中得到了广泛应用[3]。随后,Balakrishnan等人提出了著名的框架VoxelMorph及其衍生版本[2],该框架计算了在优化过程中反向传播变形误差的梯度,极大的提升了基于深度学习配准的准确率和速度。然而,由于上述方法都侧重于单模态图像配准,多对比度图像配准仍有待探索。
1.3 基于深度学习的多模态图像配准
与单模态配准相比,多模态配准更具挑战性,因为很难定义有效的相似性度量来指导不同模态的局部匹配。互信息(Mutual information,MI)是现有研究中最常用的多模态相似度指标, 然而,MI是一种局部平均算法,很难得到精确的配准结果。
1.4 本文贡献
1)本文提出了一个无监督的粗到细配准框架。首先通过仿射变换网络获得粗配准,随后通过可变形变换网络对其进行细化,实现了端到端的图像配准。
2) 设计了双重一致性约束以最大化多对比度 MR 图像的拓扑图的互相关,提升正向形变的准确性。逆变形场直接由前向变形场产生,从而允许网络对正向形变场优化。
3) 设计了基于先验知识的损失函数,以实现更准确的配准。具体而言,对目标域的背景区域中的像素使用L2约束,从而减少来自源域的错误配准像素。
2. 方法
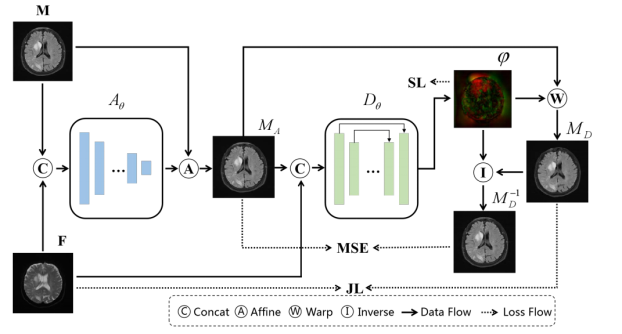
图1. 所提出的无监督粗到细配准框架及对偶一致性约束流程。其中M(Moving)表示待配准图像,F(Fixed)表示目标域图像
2.1 粗到细的无监督配准框架
为了减少无监督多对比度图像转换的挑战,作者提出了一种从粗到细的图像配准框架,如图1所示。 他们将冻结参数的预训练仿射变换网络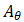 嵌入到可形变变换网络
嵌入到可形变变换网络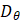 中。通过这种方式,
中。通过这种方式,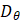 接收的图像与目标图像大致对齐,减少了后续可形变配准的困难度,从而提升了配准结果的准确率。与使用仿射变换作为预处理然后精细化预测的两步配准的现有方法不同,所提出的框架采用端到端的方法,在一个架构中一体化操作。与现有的配准方法相比,作者所提出的方法不需要迭代进行仿射或变形变换。
接收的图像与目标图像大致对齐,减少了后续可形变配准的困难度,从而提升了配准结果的准确率。与使用仿射变换作为预处理然后精细化预测的两步配准的现有方法不同,所提出的框架采用端到端的方法,在一个架构中一体化操作。与现有的配准方法相比,作者所提出的方法不需要迭代进行仿射或变形变换。
2.2 双重一致性约束的双向图像变换
本文首先提出了一种可逆操作,用以得到对配准图像的可逆变换。随后,通过对可逆变换结果的一致性约束提升正向形变的配准结果。
定义可形变操作为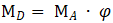 ,其中
,其中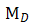 是可形变配准后图像,
是可形变配准后图像,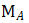 是待配准图像,
是待配准图像,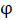 表示形变场,其大小应为
表示形变场,其大小应为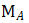 图像的(长x宽x2), 最后一维的2表示在长宽维度各自具有的偏移量,
图像的(长x宽x2), 最后一维的2表示在长宽维度各自具有的偏移量,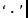 表示根据形变场偏移量所进行的形变操作。则可逆形变场可被定义为:
表示根据形变场偏移量所进行的形变操作。则可逆形变场可被定义为:
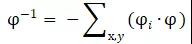
可逆变换可被表示为: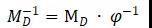
通过一致性约束最小化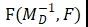 ,则能得到鲁棒的
,则能得到鲁棒的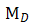 。
。
2.3 基于先验的背景抑制损失
由于医学影像的特殊性,可以通过阈值的方法简单区分背景区域和前景区域。本文作者通过这种特性,使用L2约束在目标域背景区域的错误配准像素,所使用的约束可被表示为:
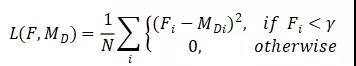
其中,N表示像素数,F表示目标域图像,是阈值参数,i表示像素下标。
3. 实验及结果
3.1 数据集及预处理
本研究总共使用了来自555名患者的数据,分别包含或不包含中风病变。每名患者都具有五种序列:T1、T2、FLAIR、ADC 和 DWI。所有图像均使用西门子1.5T扫描仪获得。在555个案例中,466个提供了扫描信息,剩余的则没有扫描信息,无法进行物理预校正。进行了两组实验,一组根据提供的扫描信息进行物理空间对齐,另一组没有。在第一组实验中,仅利用了具有扫描信息的466个案例。随机选取426个案例作为训练集,其余40个案例作为测试集。测试集的 DWI 和 FLAIR 图像中的中风病变由有经验的临床医生注释,用于定量结果评估。在第二组实验中,使用了所有555个案例。由于没有进行物理空间预对齐,89个没有扫描信息的案例被包含在训练集中。所有数据都调整为224×224,灰度归一化到[0, 1]范围。
3.2 结果展示
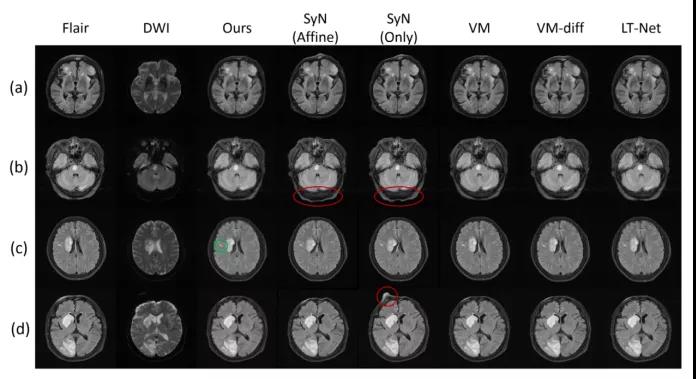
图2. 不同方法的定性分析。绿色圈表示作者的方法比其他方法配准得更好的部分,红色圈表示发生了不期望的变形
不同方法的结果如图 2 所示。(a)行中,对比算法生成了变形的头骨,作者所提出的方法可以很好地保持结构。在低信号区域,例如示例 (b)中的红圈,迭代方法 SyN显示出奇怪的变形,使组织看起来异常。在示例 (c) 中,基于深度学习的对比方法无法完全匹配中风病变。由于所提出方法设计的更强大的配准流程,仍然可以保持良好的配准。最后,当存在扫描伪影时(示例(d)),SyN显示出明显的图像失真以适应伪影。总的来说,所提出方法在具有伪影、急剧变化等具有挑战性的情况下表现特别好。
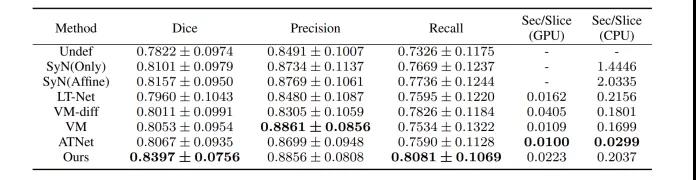
表 I. 配准结果的定量分析
定量结果列于表 I。在没有配准的情况下,FLAIR和DWI图像中的中风病变注释未对齐,平均 Dice 得分为0.7822,这反映了多对比度图像需要进行配准。ATNet(仿射变换网络)得到0.8067,反映出即使物理空间对齐,仍然需要线性变换才能实现准确配准。没有经过仿射变换的方法SyN(Only)生成类似的结果–0.8101。通过引入仿射变换 (SyN(Affine)),提高到0.8157。我们的方法获得了0.8397的最高分,证明了其在处理多对比度图像配准问题方面的有效性。作者还比较了不同方法的效率。为了公平比较,所有方法都在CPU上进行了测试。SyN(Affine)是效率最低的方法,配准一张图像需要2.0335 秒,而ATNet的效率最高,只需要0.02秒。与最具竞争力的方法SyN(Affine)相比,本文所提出的方法快了约 10 倍,且配准结果更好。它可以在5秒内实现1个3D图像病例(20个切片)的配准,有望满足临床实时诊断的需求。在GPU上进行测试时,花费的时间可以进一步缩短到0.5秒/例以内。
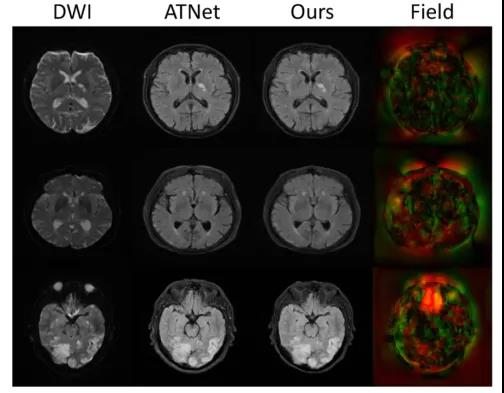
图3. 形变场的可视化分析。红色表示水平方向位移,绿色表示竖直方向的位移。更高的信号表示位移长度越大
形变场的可视化如图3所示。这些例子表明,即使在物理对齐和仿射变换之后,仍然需要可形变变换(由变换场中的红色和绿色信号表示)。因此,在应用中同时需要物理对齐、仿射变换和可变形变换,尤其是后两者。
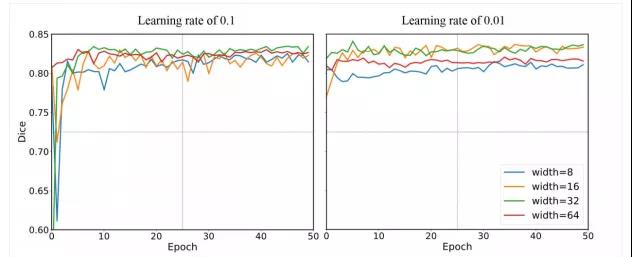
图4. 不同的学习率和网络宽度对应的配准结果分析
在图4中,作者展示了在两种学习率下具有不同宽度的网络的脑卒中配准得分。虽然较大的学习率可以使得收敛更快,但波动的Dice得分曲线表明训练是不稳定的。特别是对于宽度为32的网络,较小的学习率可能更合适。对于不同的网络宽度,观察到宽度为8和16时的性能明显更差,这可能表明网络无法捕获复杂的图像属性。宽度为32和64的更宽的网络表现出相似的性能,宽度为32的网络性能稍好。值得注意的是,在所有实现中都没有过拟合,这间接证明了我们的方法适用于多对比度图像配准任务。

表II. 可逆方法所需时间的定量分析
为了研究所提出的逆变换的效率,作者将提出的方法的时间消耗与现有的逆方法VM-diff和LT-Net进行了比较。使用相同的神经网络 (DTNet) 实现了所有方法。所提出方法是最快的
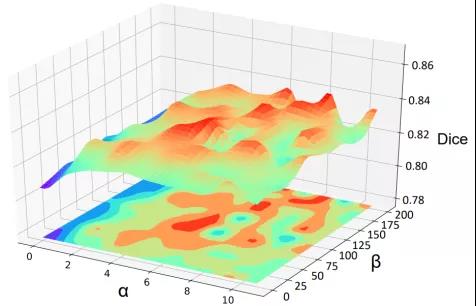
图5. 不同的损失函数权值(α和β)对配准性能的影响
作者对多种损失函数权重进行了消融实验,如图5所示。图中α表示MI损失的权重,β表示所提出的区域抑制损失。实验结果证明了所提出方法对于损失权重超参数的设置具有鲁棒性。
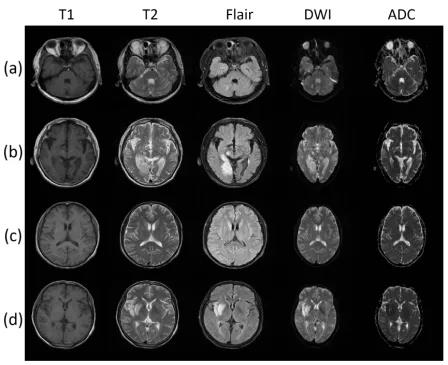
图6. MRI的多对比度图像(没有提前进行物理空间对齐),每一行表示来自同一层的不同对比度图像。每行图像之间的形态展示了巨大的差异。
临床核磁共振影像数据有时会因为不可避免的问题丢失扫描信息,包括像素间距和视野。没有扫描信息,就无法在物理空间中对多对比度图像进行预对齐,这给准确的图像配准任务带来了很大的困难。为了提高所提出方法的应用能力,作者在没有第一步物理空间对齐的情况下进行了实验。在这组实验中,使用了所有收集的555个图像数据。一些例子如图6所示。可以观察到,由于成像参数不同,不同对比度图像之间存在较大差异。
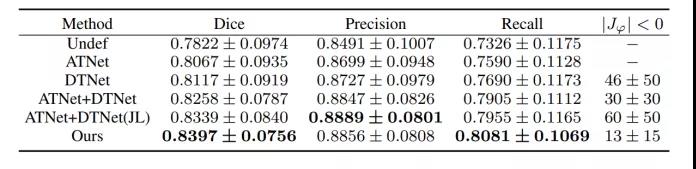
表III. 更困难数据集的定量分析
针对这些更困难数据集的定量分析如表III所示。在没有进行任何配准之前(物理对齐),FLAIR和DWI图像中的中风病变标注在很大程度上未对齐,平均Dice得分仅为0.3472。与第一步物理空间对齐(表 I)获得的分数相比,SyN(Only)的性能显着降低了20%以上(0.5880对0.8101)。SyN(Affine)的得分略有下降,为0.8048。所有基于学习的比较方法的分数下降了大约4%。本文的方法仍然保持良好的性能,得分为0.8260,仅下降了 1.37%。这表明所提出的方法对困难的任务具有很好的鲁棒性。在时间需求上,所提出的方法比耗时的基于迭代的SyN(Affine)方法更好。总体而言,当面临更具挑战性的任务时,本文的方法仍然可以保持良好的配准性能,且配准速度令人满意。
4. 总结
多对比度MR图像配准对于许多临床应用至关重要,而现有的配准方法在多对比度MR图像配准方面受到性能或速度的限制。本文提出了一种新的基于无监督深度学习的配准框架,与SOTA的配准方法相比,性能优异。
所提方法不仅限于多对比度MR图像配准。它还可以通过修改应用于单模态或其他多模态图像配准任务。此外,当人工标注的获取成本很高并且需要减少对标注的依赖时,可以在基于学习的方法的开发中采用准确有效的配准算法。例如,所提出的方法可以很容易地扩展到基于图谱的分割任务。
5. 讨论
这篇文章基于2D层级完成了对MRI多对比度影像的配准,获得了较好的效果。由于MRI数据是三维的,基于3D的配准可能还能进一步提升配准性能。作为展望,如何平衡3D空间配准所需要的资源消耗和性能仍有值得研究的意义。
参考文献
[1] Avants, B. B., Epstein, C. L., Grossman, M., and Gee, J. C. “Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain.” Medical image analysis 12.1 (2008): 26-41.
[2] G. Balakrishnan, A. Zhao, M. R. Sabuncu, J. Guttag, and A. V. Dalca, “Voxelmorph: a learning framework for deformable medical image registration,” IEEE transactions on medical imaging, vol. 38, no. 8, pp. 1788–1800, 2019.
[3] M. Jaderberg, K. Simonyan, A. Zisserman, and k. kavukcuoglu, “Spatial transformer networks,” in Advances in Neural Information Processing Systems 28, C. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, and R. Garnett, Eds. Curran Associates, Inc., 2015, pp. 2017–2025.
本文作者:黄纬键(深圳先进技术研究院)
指导教师:王珊珊(深圳先进技术研究院)
编辑:秘书处


 关注微信公众号
关注微信公众号